Euclid's The Elements

Understanding the Greek Euclid's basic first three proofs of the Elements, is to understand the basics of math.

The Elements (Ancient Greek: Στοιχεῖον Stoikheîon) is a mathematical treatise consisting of 13 books attributed to the ancient Greek mathematician Euclid in Alexandria, Ptolemaic Egypt c. Euclid's Elements has been referred to as the most successful and influential textbook ever written. The ancient Greek mathematician Euclid of Alexandria, educated in Ptolemaic Egypt from the timeframe 300 BC.

A mathematical treatise consisting of 13 books, is instrumental in the development of logic and modern science.

Euclid's The Elements Contents

• Book 1 contains 5 postulates (including the famous parallel postulate) and 5 common notions and covers important topics of plane geometry such as the Pythagorean theorem, equality of angles and areas, parallelism, the sum of the angles in a triangle, and the construction of various geometric figures.
• Book 2 contains a number of lemmas concerning the equality of rectangles and squares, sometimes referred to as "geometric algebra", and concludes with the construction of the golden ratio and a way of constructing a square equal in area to any rectilinear plane figure.
• Book 3 deals with circles and their properties: finding the center, inscribed angles, tangents, the power of a point, Thales' theorem.
• Book 4 constructs the incircle and circumcircle of a triangle, as well as regular polygons with 4, 5, 6, and 15 sides.
• Book 5, on proportions of magnitudes, gives the highly sophisticated theory of proportion probably developed by Eudoxus, and proves properties such as "alternation" (if a : b :: c : d, then a : c :: b : d).
• Book 6 applies proportions to plane geometry, especially the construction and recognition of similar figures.
• Book 7 deals with elementary number theory: divisibility, prime numbers and their relation to composite numbers, Euclid's algorithm for finding the greatest common divisor, finding the least common multiple.
• Book 8 deals with the construction and existence of geometric sequences of integers.
• Book 9 applies the results of the preceding two books and gives the infinitude of prime numbers and the construction of all even perfect numbers.
• Book 10 proves the irrationality of the square roots of non-square integers (e.g. {\displaystyle {\sqrt {2}}}) and classifies the square roots of incommensurable lines into thirteen disjoint categories. Euclid here introduces the term "irrational", which has a different meaning than the modern concept of irrational numbers. He also gives a formula to produce Pythagorean triples.^[14]
• Book 11 generalizes the results of book 6 to solid figures: perpendicularity, parallelism, volumes and similarity of parallelepipeds.
• Book 12 studies the volumes of cones, pyramids, and cylinders in detail by using the method of exhaustion, a precursor to integration, and shows, for example, that the volume of a cone is a third of the volume of the corresponding cylinder. It concludes by showing that the volume of a sphere is proportional to the cube of its radius (in modern language) by approximating its volume by a union of many pyramids.
• Book 13 constructs the five regular Platonic solids inscribed in a sphere and compares the ratios of their edges to the radius of the sphere.

An animation showing how Euclid constructed a hexagon (Book IV, Proposition 15). Every two-dimensional figure in the Elements can be constructed using only a compass and straightedge.

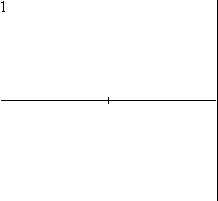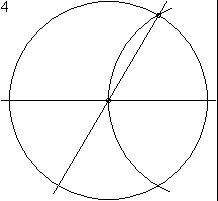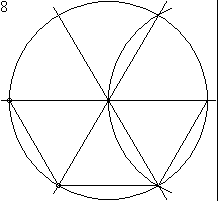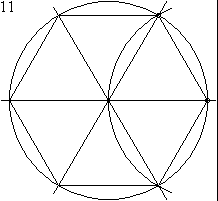
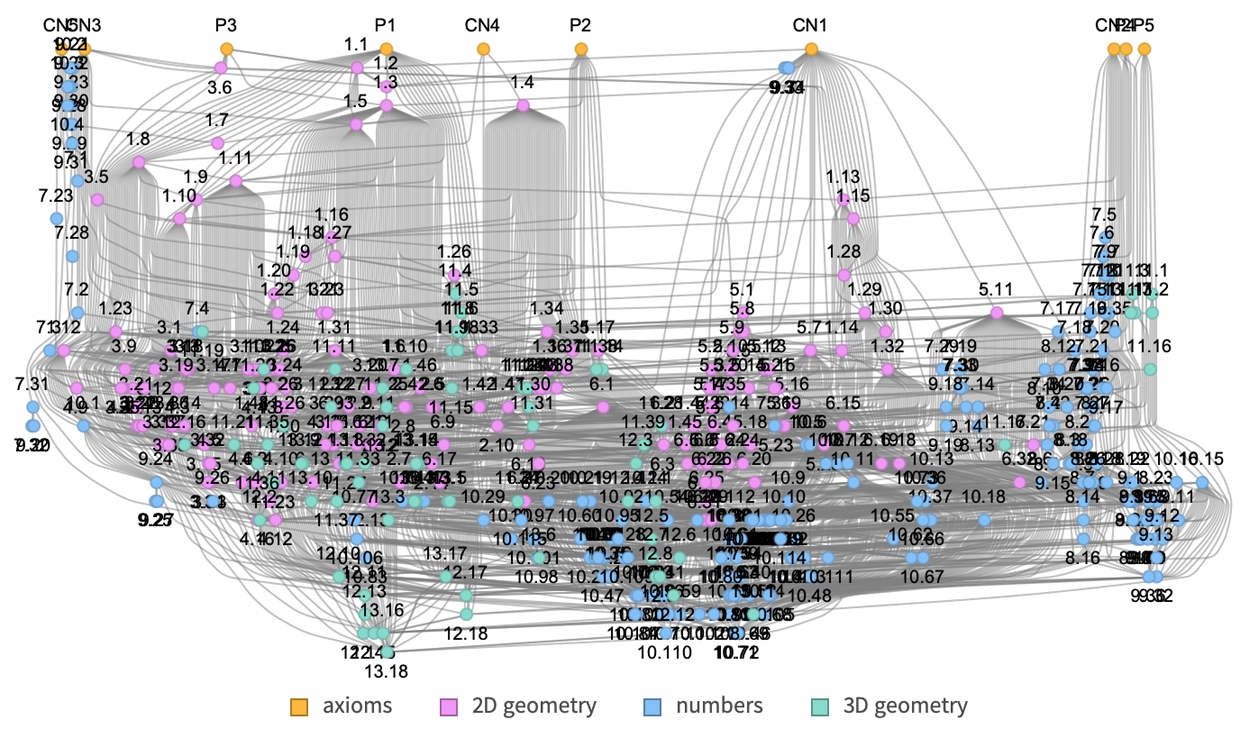
And below is a table to describe Propositions plotted with lines connected from Axioms on the top and other preceding propositions, labeled by The Elements book.